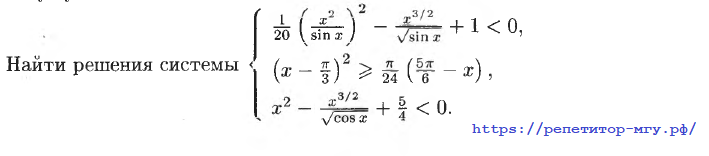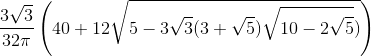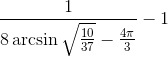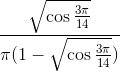- Математический кружок для 8-9кл.: развитие способностей/увлеченности решать нестандартные, логические, интересные задачи.
- Подготовка к математическим олимпиадам «Ломоносов»,«Покори Воробьевы горы».
- Подготовка к сдаче Основного государственного экзамена выпускников 9 классов (ОГЭ).
- Подготовка к сдаче Единого государственного экзамена (ЕГЭ).
- Подготовка к сдаче Дополнительных вступительных испытаний(ДВИ) в МГУ имени М.В.Ломоносова.
по экзаменам в МГУ с 1965г.), высокий уровень подготовки.
Опыт преподавания ученикам с 1972г.(будучи еще на 1-м курсе ВМК), абитуриентам с 1973г.
Опыт приема вступительных экзаменов в МГУ (в качестве проверяющего работы) с 1980г.
по настоящее время.
Обращаться к преподавателю.